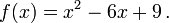어떤 함수의 zero 라는 건 함수값이 0 이 되는 그 함수 정의역 위의 점을 말한다. 처음 이 용어 볼 때 해석하느라 혼란스러웠음..
Root (mathematics)
From Wikipedia, the free encyclopedia
- This article is about the zeros of a function, which should not be confused with the value at zero. You may also want information on the Nth roots of numbers instead.
In mathematics, a root (or a zero) of a complex-valued function ƒ is a member x of the domain of ƒ such that ƒ(x) vanishes at x, that is,
in other words, a "root" of a function f is a value for x that produces a result of zero ("0"). For example, consider the function f defined by the following formula:
This function has a root at 3 because f(3) = 32 − 6(3) + 9 = 0.
If the function is mapping from real numbers to real numbers, its zeros are the points where its graph meets the x-axis. The x-value of such a point is called x-intercept. Therefore in this situation a root can be called an x-intercept.
The word root can also refer to the nth root of a number, a, as in ![a^{1/n} = \sqrt[n]{a}](http://upload.wikimedia.org/math/b/f/e/bfe2bc3041d3919d6ff446fce95e19f7.png) . The square root of a number, a, is
. The square root of a number, a, is ![a^{1/2} = \sqrt[2]{a} = \sqrt{a}](http://upload.wikimedia.org/math/6/5/9/659ef5c0d62e9a2d6c0b098ef7dc2042.png) .
.
(하략)
'수학 관련' 카테고리의 다른 글
| Nomalized Cross Correlation (0) | 2012.04.04 |
|---|---|
| Scalar Field, Vector Field, Scalar Potential (0) | 2011.07.13 |
| 쿼터니언(Quaternion) (0) | 2011.07.01 |
| Dimension (0) | 2010.06.22 |
| 옛날엔, 연속인 함수가 적어도 유한개의 점에서만 미분 불가능이라고 생각했었다. (0) | 2009.10.15 |